Contrastive Learning Inverts the Data Generating Process

Roland S Zimmermann*, Yash Sharma*, Steffen Schneider*, Matthias Bethge, Wieland Brendel

June 2021

Abstract

Contrastive learning has recently seen tremendous success in self-supervised learning. So far, however, it is largely unclear why the learned representations generalize so effectively to a large variety of downstream tasks. We here prove that feedforward models trained with objectives belonging to the commonly used InfoNCE family learn to implicitly invert the underlying generative model of the observed data. While the proofs make certain statistical assumptions about the generative model, we observe empirically that our findings hold even if these assumptions are severely violated. Our theory highlights a fundamental connection between contrastive learning, generative modeling, and nonlinear independent component analysis, thereby furthering our understanding of the learned representations as well as providing a theoretical foundation to derive more effective contrastive losses.

Publication

ICML 2021

Contributions

We establish a theoretical connection between the InfoNCE family of objectives, which is commonly used in self-supervised learning, and nonlinear ICA. We show that training with InfoNCE inverts the data generating process if certain statistical assumptions on the data generating process hold.
We empirically verify our predictions when the assumed theoretical conditions are fulfilled. In addition, we show successful inversion of the data generating process even if theoretical assumptions are partially violated.
We build on top of the CLEVR rendering pipeline (Johnson et al., 2017) to generate a more visually complex disentanglement benchmark, called 3DIdent, that contains hallmarks of natural environments (shadows, different lighting conditions, a 3D object, etc.). We demonstrate that a contrastive loss derived from our theoretical framework can identify the ground-truth factors of such complex, high-resolution images.

Theory

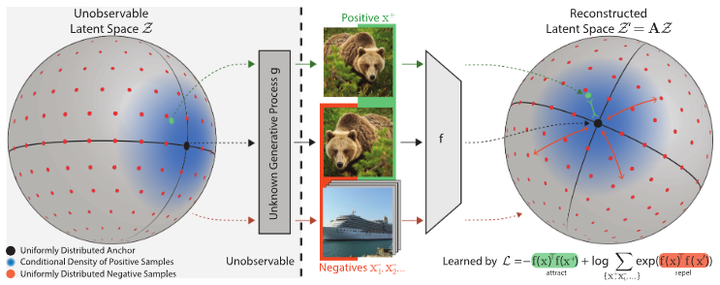
We start with the well-known formulation of a contrastive loss (often called InfoNCE),

$$ \newcommand{\xx}{\mathbf{x}} \newcommand{\tx}{\tilde{\mathbf{x}}} L(f; \tau, M) := \underset{\substack{ (\xx, \tx) \sim p_\mathsf{pos} \\ \{\xx^-_i\}_{i=1}^M \overset{\text{i.i.d.}}{\sim} p_\mathsf{data} }}{\mathbb{E}} \left[\, {- \log \frac{e^{f(\xx)^{\mathsf{T}} f(\tx) / \tau }}{e^{f(\xx)^{\mathsf{T}} f(\tx) / \tau } + \sum\limits_{i=1}^M e^{f(\xx^-_i)^{\mathsf{T}} f(\tx) / \tau }}}\,\right]. \nonumber $$

Our theoretical approach consists of three steps:

We demonstrate that the contrastive loss (L) can be interpreted as the cross-entropy between the (conditional) ground-truth and an inferred latent distribution.
Next, we show that encoders minimizing the contrastive loss maintain distance, i.e., two latent vectors with distance (\alpha) in the ground-truth generative model are mapped to points with the same distance (\alpha) in the inferred representation.
Finally, we use distance preservation to show that minimizers of the contrastive loss (L) invert the generative process up to certain invertible linear transformations.

We follow this approach both for the contrastive loss (L) defined above, and use our theory as a starting point to design new contrastive losses (e.g., for latents within a hypercube). We validate predictions regarding identifiability of the latent variables (up to a transformation) with extensive experiments.

Dataset

We introduce 3Dident, a dataset with hallmarks of natural environments (shadows, different lighting conditions, 3D rotations, etc.). We publicly released the full dataset (including both, the train and test set) here. Reference code for evaluation has been made available at our repository .

3DIdent: Influence of the latent factors $\mathbf{z}$ on the renderings $\mathbf{x}$. Each column corresponds to a traversal in one of the ten latent dimensions while the other dimensions are kept fixed.